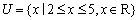2025年上海高考数学试题及答案
（考试时间120分钟，满分150分）
一、填空题（本大题共12题，第1~6题每题4分，第7~12题每题5分，共54分.考生应在答题纸的相应位置直接填写结果）
1．已知全集
，集合，则 ．
2．不等式的解集为 ．
3．己知等差数列的首项，公差，则该数列的前6项和为 ．
4．在二项式的展开式中，的系数为 ．
5．函数在上的值域为 ．
6．已知随机变量X的分布为，则期望 ．
7．如图，在正四棱柱中，，则该正四棱柱的体积为 ．
8．设，则的最小值为 ．
9．4个家长和2个儿童去爬山，6个人需要排成一条队列，要求队列的头和尾均是家长，则不同的排列个数有 种．
10．已知复数z满足，则的最小值是 ．
11．小申同学观察发现，生活中有些时候影子可以完全投射在斜面上．某斜面上有两根长为1米的垂直于水平面放置的杆子，与斜面的接触点分别为A、B，它们在阳光的照射下呈现出影子，阳光可视为平行光：其中一根杆子的影子在水平面上，长度为0.4米；另一根杆子的影子完全在斜面上，长度为0.45米．则斜面的底角 ．（结果用角度制表示，
精确到）
12．已知，是平面内三个不同的单位向量．若，则可的取值范围是 ．
二、选择题（本大题共4题，第13、14题每题4分，第15、16题每题5分，共18分.每题有且仅有一个正确选项，考生应在答题纸的相应位置，将代表正确选项的小方格涂黑.）
13．己知事件A、B相互独立，事件A发生的概率为，事件B发生的概率为，则事件发生的概率为（ ）
A．B．C．D．0
14．设．下列各项中，能推出的一项是（ ）
A．，且B．，且
C．，且D．，且
15．已知，C在上，则的面积（ ）
A．有最大值，但没有最小值B．没有最大值，但有最小值
C．既有最大值，也有最小值D．既没有最大值，也没有最小值
16．已知数列、、的通项公式分别为，、，.若对任意的，、、的值均能构成三角形，则满足条件的正整数有（ ）
A． 4个B．3个C．1个D．无数个
三、解答题（本大题共5题，第17-19题每题14分，第20-21题每题18分，共78分.解答下列各题必须在答题纸的相应位置写出必要的步骤.）
17．2024年东京奥运会，中国获得了男子米混合泳接力金牌．以下是历届奥运会男子米混合泳接力项目冠军成绩记录（单位：秒），数据按照升序排列
206.78 | 207.46 | 207.95 | 209.34 | 209.35 |
210.68 | 213.73 | 214.84 | 216.93 | 216.93 |
(1)求这组数据的极差与中位数；
(2)从这10个数据中任选3个，求恰有2个数据在211以上的概率；
(3)若比赛成绩y关于年份x的回归方程为，年份x的平均数为2006，预测2028年冠军队的成绩（精确到0.01秒）．
18．如图，P是圆锥的顶点，O是底面圆心，AB是底面直径，且．
(1)若直线PA与圆锥底面的所成角为，求圆锥的侧面积；
(2)已知Q是母线PA的中点，点C、D在底面圆周上，且弧AC的长为，．设点M在线段OC上，证明：直线平面PBD．
19．已知．
(1)若，求不等式的解集；
(2)若函数满足在上存在极大值，求m的取值范围；
20．已知椭圆，，A是的右顶点．
(1)若的焦点，求离心率e；
(2)若，且上存在一点P，满足，求m；
(3)已知AM的中垂线l的斜率为2，l与交于C、D两点，为钝角，求a的取值范围．
21．已知函数的定义域为．对于正实数a，定义集合．
(1)若，判断是否是中的元素，请说明理由；
(2)若，求a的取值范围；
(3)若是偶函数，当时，，且对任意，均有．写出，解析式，并证明：对任意实数c，函数在上至多有9个零点．
参考答案
1．##
2．
3．
4．
5．
6．
7．
8．4
9．288
10．
11．
12．
13．B
14．D
15．A
16．B
17．
(1)；；
(2)
(3)
18．
(1)
（2）由题知，则根据中位线性质，，
又平面，平面，则平面
由于，底面圆半径是，则，又，则，
又，则为等边三角形，则，
于是且，则四边形是平行四边形，故，
又平面，平面，故平面
又平面，
根据面面平行的判定，于是平面平面，
又，则平面，则平面
19．
(1)
(2)且.
20．
(1)
(2)
(3)
21．
(1)不是；
(2)；
（3）（3）对任意，因为其是偶函数，
则，而，
所以，
所以，因为，则，
所以，所以，
所以当时，，，则，
，则，
而，，
则，则，
所以当时，，而为偶函数，画出函数图象如下：
其中，但其对应的值均未知.
首先说明，
若，则，易知此时，
则，所以，而时，，
所以，与矛盾，所以，即，
令，则，
当时，即使让，此时最多7个零点，
当时，若，此时有5个零点，
故此时最多5个零点；
当时，若，此时有5个零点，
故此时最多5个零点；
当时，若，此时有3个零点，
若，则，易知此时，
则，所以，而时，，
所以，与矛盾，所以，
则最多在之间取得6个零点，
以及在处成为零点，故不超过9个零点.
综上，零点不超过9个.
