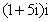2025年福建高考数学试题及答案
一、选择题：本大题共8小题，每小题5分，共计40分.每小题给出的四个选项中，只有一个选项是正确的.请把正确的选项填涂在答题卡相应的位置上.
1. 
的虚部为（ ）
A B. 0C. 1D. 6
2. 设全集，集合，则中元素个数为（ ）
A. 0B. 3C. 5D. 8
3. 若双曲线C的虚轴长为实轴长的倍，则C的离心率为（ ）
A. B. 2C. D.
4. 若点是函数的图象的一个对称中心，则a的最小值为（ ）
A. B. C. D.
5. 设是定义在上且周期为2偶函数，当时，，则（ ）
A. B. C. D.
6. 帆船比赛中，运动员可借助风力计测定风速的大小和方向，测出的结果在航海学中称为视风风速，视风风速对应的向量，是真风风速对应的向量与船行风速对应的向量之和，其中船行风速对应的向量与船速对应的向量大小相等，方向相反.图1给出了部分风力等级、名称与风速大小的对应关系.已知某帆船运动员在某时刻测得的视风风速对应的向量与船速对应的向量如图2（风速的大小和向量的大小相同），单位（m/s），则真风为（ ）
等级 | 风速大小m/s | 名称 |
2 | 1.1~3.3 | 轻风 |
3 | 3.4~5.4 | 微风 |
4 | 5.5~7.9 | 和风 |
5 | 8.0~10.1 | 劲风 |
A. 轻风B. 微风C. 和风D. 劲风
7. 若圆上到直线的距离为1的点有且仅有2个，则r的取值范围是（ ）
A. B. C. D.
8. 若实数x，y，z满足，则x，y，z的大小关系不可能是（ ）
A. B.
C. D.
二、选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.
9. 在正三棱柱中，D为BC中点，则（ ）
A. B. 平面
C. 平面D.
10. 设抛物线的焦点为F，过F的直线交C于A、B，过F且垂直于的直线交于E，过点A作准线l的垂线，垂足为D，则（ ）
A. B.
C D.
11. 已知的面积为，若，则（ ）
A. B.
C. D.
三、填空题：本大题共3小题，每小题5分，共计15分.
12. 若直线是曲线的切线，则_________.
13. 若一个等比数列前4项和为4，前8项和为68，则该等比数列的公比为_________.
14. 一个箱子里有5个相同的球，分别以1~5标号，若有放回地取三次，记至少取出一次的球的个数X，则数学期望_________.
四、解答题：本题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤.
15. 为研究某疾病与超声波检查结果的关系，从做过超声波检查的人群中随机调查了1000人，得到如下列联表：
超声波检查结果 组别 | 正常 | 不正常 | 合计 |
患该疾病 | 20 | 180 | 200 |
未患该疾病 | 780 | 20 | 800 |
合计 | 800 | 200 | 1000 |
（1）记超声波检查结果不正常者患该疾病的概率为P，求P的估计值；
（2）根据小概率值的独立性检验，分析超声波检查结果是否与患该疾病有关.
附，
| 0.005 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
16. 设数列满足，
（1）证明：为等差数列；
（2）设，求．
17. 如图所示的四棱锥中，平面，．
（1）证明：平面平面；
（2），，，，在同一个球面上，设该球面的球心为．
（i）证明：在平面上；
（ⅱ）求直线与直线所成角的余弦值．
18. 设椭圆的离心率为，下顶点为A，右顶点为B，．
（1）求椭圆的标准方程；
（2）已知动点P不在y轴上，点R在射线AP上，且满足．
（i）设，求点的坐标（用m，n表示）；
（ⅱ）设O为坐标原点，是椭圆上的动点，直线OR的斜率为直线的斜率的3倍，求的最大值．
19. 设函数．
（1）求在的最大值；
（2）给定，设a实数，证明：存在，使得；
（3）若存在使得对任意x，都有，求b的最小值
参考答案
一、选择题：本大题共8小题，每小题5分，共计40分.每小题给出的四个选项中，只有一个选项是正确的.请把正确的选项填涂在答题卡相应的位置上.
【1题答案】
【答案】C
【2题答案】
【答案】C
【3题答案】
【答案】D
【4题答案】
【答案】C
【5题答案】
【答案】A
【6题答案】
【答案】A
【7题答案】
【答案】B
【8题答案】
【答案】B
二、选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.
【9题答案】
【答案】BC
【10题答案】
【答案】ACD
【11题答案】
【答案】ABC
三、填空题：本大题共3小题，每小题5分，共计15分.
【12题答案】
【答案】
【13题答案】
【答案】
【14题答案】
【答案】##
四、解答题：本题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤.
【15题答案】
【答案】（1）
（2）有关
【16题答案】
【答案】
（1）
由题意证明如下，，
在数列中，，，
∴，即，
∴是以为首项，1为公差的等差数列.
（2）
【17题答案】
【答案】
（1）
由题意证明如下，
在四棱锥中，⊥平面，，
平面，平面，
∴，，
∵平面，平面，，
∴平面，
∵平面，
∴平面平面
（2）（i）；
（ii）.
【18题答案】
（1）
（2）(ⅰ) (ⅱ)
【19题答案】
（1）
（2）
法1：由余弦函数的性质得的解为，，
若任意与交集空，
则且，此时无解，
矛盾，故无解；故存在，使得，
法2：由余弦函数的性质知的解为，
若每个与交集都为空，
则对每个，必有或之一成立.
此即或，但长度为的闭区间上必有一整数，该整数不满足条件，矛盾.
故存在，使得成立
（3）
