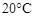2024年海南中考数学试题及答案
一、选择题（本大题满分36分，每小题3分）在下列各题的四个备选答案中，有且只有一个是正确的，请在答题卡上把你认为正确的答案的字母代号按要求用2B铅笔涂黑．
1．负数的概念最早记载于我国古代著作《九章算术》．若零上
记作，则零下应记作（ ）
A． B． C． D．
2．福建舰是我国首艘完全自主设计建造的电磁弹射型航空母舰，满载排水量8万余吨，数据80000用科学记数法表示为（ ）
A． B． C． D．
3．若代数式的值为5，则x等于（ ）
A．8 B． C．2 D．
4．下图是由两块完全相同的长方体木块组成的几何体，其左视图为（ ）
A． B． C． D．
5．下列计算中，正确的是（ ）
A． B． C． D．
6．分式方程的解是（ ）
A． B． C． D．
7．平面直角坐标系中，将点A向右平移3个单位长度得到点，则点A的坐标是（ ）
A． B． C． D．
8．设直角三角形中一个锐角为x度（），另一个锐角为y度，则y与x的函数关系式为（ ）
A． B． C． D．
9．如图，直线，把一块含角的直角三角板按如图所示的方式放置，点B在直线n上，，若，则等于（ ）
A． B． C． D．
10．如图，菱形的边长为2，，边在数轴上，将绕点A顺时针旋转，点C落在数轴上的点E处，若点E表示的数是3，则点A表示的数是（ ）
A．1 B． C．0 D．
11．如图，是半圆O的直径，点B、C在半圆上，且，点P在上，若，则等于（ ）
A． B． C． D．
12．如图，在中，，以点D为圆心作弧，交于点M、N，分别以点M、N为圆心，大于为半径作弧，两弧交于点F，作直线交于点E，若，则四边形的周长是（ ）
A．22 B．21 C．20 D．18
二、填空题（本大题满分12分，每小题3分）
13．因式分解： ．
14．某型号蓄电池的电压U（单位：V）为定值，使用蓄电池时，电流I（单位：A）与电阻R（单位：）是反比例函数关系，即，它的图象如图所示，则蓄电池的电压U为 （V）．
15．如图是跷跷板示意图，支柱经过的中点O，与地面垂直于点M，，当跷跷板的一端A着地时，另一端B离地面的高度为 ．
16．如图，矩形纸片中，，点E、F分别在边上，将纸片沿折叠，使点D的对应点在边上，点C的对应点为，则的最小值为 ，CF的最大值为 ．
三、解答题（本大题满分72分）
17．（1）计算：；
（2）解不等式组：．
18．端午节是中国传统节日，人们有吃粽子的习俗．某商店售卖某品牌瘦肉粽和五花肉粽．请依据以下对话，求促销活动前每个瘦肉粽、五花肉粽的售价．
19．根据以下调查报告解决问题．
调查主题 | 学校八年级学生视力健康情况 | |
背景介绍 | 学生视力健康问题引起社会广泛关注．某学习小组为了解本校八年级学生视力情况，随机收集部分学生《视力筛查》数据． | |
调查结果 | ||
八年级学生右眼视力领数分布表 |
| |
右眼视力 | 频数 | |
| 3 | |
| 24 | |
| 18 | |
| 12 | |
| 9 | |
| 9 | |
| 15 | |
合计 | 90 | |
建议：…… | ||
（说明：以上仅展示部分报告内容）
(1)本次调查活动采用的调查方式是________（填写“普查”或“抽样调查”）：
(2)视力在“”是视力“最佳矫正区”，该范围的数据为：，这组数据的中位数是________；
(3)视力低于属于视力不良，该校八年级学生有600人，估计该校八年级右眼视力不良的学生约为_______人；
(4)视力在“”范围有两位男生和一位女生，从中随机抽取两位学生采访，恰好抽到两位男生的概率是________；
(5)请为做好近视防控提一条合理的建议．
20．木兰灯塔是亚洲最高、世界第二高的航标灯塔，位于海南岛的最北端，是海南岛东北部最重要的航标．某天，一艘渔船自西向东（沿方向）以每小时10海里的速度在琼州海峡航行，如图所示．
航行记录记录一：上午8时，渔船到达木兰灯塔P北偏西 记录二：上午8时30分，渔船到达木兰灯塔P北偏西 记录三：根据气象观测，当天凌晨4时到上午9时，受天文大潮和天气影响，琼州海峡C点周围5海里内，会出现异常海况，点C位于木兰灯塔P北偏东 |
请你根据以上信息解决下列问题：
(1)填空：________，________， ________海里；
(2)若该渔船不改变航线与速度，是否会进入“海况异常”区，请计算说明．
（参考数据：）
21．如图1，抛物线经过点、，交y轴于点，点P是抛物线上一动点．
(1)求该抛物线的函数表达式；
(2)当点P的坐标为时，求四边形的面积；
(3)当时，求点P的坐标；
(4)过点A、O、C的圆交抛物线于点E、F，如图2．连接，判断的形状，并说明理由．
22．正方形中，点E是边上的动点（不与点B、C重合），，，交于点H，交延长线于点G
(1)如图1，求证：；
(2)如图2，于点P，交于点M．
①求证：点P在的平分线上；
②当时，猜想与的数量关系，并证明；
③作于点N，连接，当时，若，求的值．
参考答案
1．A
2．B
3．A
4．B
5．C
6．A
7．C
8．D
9．D
10．D
11．B
12．A
13．
14．64
15．80
16． 6
17．（1）；（2）
18．促销活动前每个瘦肉粽的售价为15元，则促销活动前每个五花肉粽的售价10元．
19．(1)抽样调查；
(2)；
(3)；
(4)；
(5)建议学校加强电子产品进校园及使用的管控．
20．
(1)30；75；5
(2)该渔船不改变航线与速度，会进入“海况异常”区
21．
(1)
(2)16
(3)或
(4)是等边三角形
22．(1)见解析；
(2)①见解析；②；③．
【详解】（1）证明：∵正方形，
∴，
∵，
∴，
∵，，
∴；
（2）①证明：连接，
由（1）得，
∴，
∴，即，
∵，
∴是等腰直角三角形，
∵，
∴，，
∵，
∴四点共圆，
∴，
∵，，
∴点P在的平分线上；
