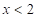2023年四川乐山中考数学试题及答案
第I卷（选择题 共30分）
注意事项：
1．选择题必须使用2B铅笔将答案标号填涂在答题卡对应题目标号的位置上。
2．在每小题给出的四个选项中，只有一个选项符合题目要求。
一、选择题：本大题共10个小题，每小题3分，共30分。
1．计算：
（ ）
A．a B． C． D．1
2．下面几何体中，是圆柱的为（ ）
A． B． C． D．
3．下列各点在函数图象上的是（ ）
A． B． C． D．
4．从水利部长江水利委员会获悉，截止2023年3月30日17时，南水北调中线一期工程自2014年12月全面通水以来，已累计向受水区实施生态补水约90亿立方米．其中9000000000用科学记数法表示为（ ）
A． B． C． D．
5．乐山是一座著名的旅游城市，有着丰富的文旅资源．某校准备组织初一年级500名学生进行研学旅行活动，政教处周老师随机抽取了其中50名同学进行研学目的地意向调查，并将调查结果制成如下统计图，如图所示估计初一年级愿意去“沫若故居”的学生人数为（ ）
A．100 B．150 C．200 D．400
6．如图2，菱形ABCD的对角线AC与BD相交于点O，E为边BC的中点，连结OE．若，则（ ）
A．2 B． C．3 D．4
7．若关于x的一元二次方程两根为，且，则m的值为（ ）
A．4 B．8 C．12 D．16
8．我国汉代数学家赵爽在注解《周髀算经》时给出“赵爽弦图”，如图所示，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形．如果大正方形面积为25，小正方形面积为1，则（ ）
A． B． C． D．
9．如图，抛物线经过点，且，有下列结论：①；②；③；④若点在抛物线上，则．其中，正确的结论有（ ）
A．4个 B．3个 C．2个 D．1个
10．如图5，在平面直角坐标系中，直线与x轴、y轴分别交于A、B两点，C、D是半径为1的上两动点，且，P为弦CD的中点．当C、D两点在圆上运动时，面积的最大值是（ ）
A．8 B．6 C．4 D．3
第Ⅱ卷（非选择题 共120分）
注意事项：
1．考生使用0.5m黑色墨汁签字笔在答题卡上题目所指示的答题区域内作答，答在试题卷上无效。
2．作图时，可先用铅笔画线，确认后再用0.5mm黑色墨汁签字笔描清楚。
3．解答题应写出文字说明、证明过程或推演步骤。
4．本部分共16个小题，共120分。
二、填空题：本大题共6个小题，每小题3分，共18分。
11．不等式的解集是__________．
12．小张在“阳光大课间”活动中进行了5次一分钟跳绳练习，所跳个数分别为：160，163，160，157，160．这组数据的众数为__________．
13．如图，点O在直线AB上，OD是的平分线，若，则的度数为__________．
14．若m、n满足，则__________．
15．如图，在平行四边形ABCD中，E是线段AB上一点，连结AC、DE交于点F．若，则__________．
16．定义：若x，y满足且（t为常数），则称点为“和谐点”．
（1）若是“和谐点”，则__________．
（2）若双曲线存在“和谐点”，则k的取值范围为__________．
三、解答题：本大题共10个小题，共102分。解答应写出必要的文字说明，证明过程或演算步骤。
17．（本小题满分9分）
计算：
18．（本小题满分9分）
解二元一次方程组：
19．（本小题满分9分）
如图，已知AB与CD相交于点O，，求证：．
20．（本小题满分10分）
如图9，在中，，点D为AB边上任意一点（不与点A、B重合），过点D作，，分别交AC、BC于点E、F，连结EF．
（1）求证：四边形ECFD是矩形；
（2）若，求点C到EF的距离．
21．（本小题满分10分）
为了践行习近平总书记提出的“绿水青山就是金山银山”的发展理念，某地计划在规定时间内种植梨树6000棵．开始种植时，由于志愿者的加入，实际每天种植梨树的数量比原计划增加了，结果提前2天完成任务．问原计划每天种植梨树多少棵？
22．（本小题满分10分）
为培养同学们爱劳动的习惯，某班开展了“做好一件家务”主题活动，要求全班同学人人参与经统计，同学们做的家务类型为“洗衣”“拖地”“煮饭”“刷碗”．班主任将以上信息绘制成了统计图表，如图所示
家务类型 | 洗衣 | 拖地 | 煮饭 | 刷碗 |
人数（人） | 10 | 12 | 10 | m |
根据上面图表信息，回答下列问题：
（1）__________；
（2）在扇形统计图中，“拖地”所占的圆心角度数为__________；
（3）班会课上，班主任评选出了近期做家务表现优异的4名同学，其中有2名男生．现准备从表现优异的同学中随机选取两名同学分享体会，请用画树状图或列表的方法求所选同学中有男生的概率．
23．（本小题满分10分）
如图，一次函数的图象与反比例函数的图象交于点，与x轴交于点B， 与y轴交于点．
（1）求m的值和一次函数的表达式；
（2）已知P为反比例函数图象上的一点，，求点P的坐标．
24．（本小题满分10分）
如图，已知是的外接圆，，D是圆上一点，E是DC延长线上一点，连结AD，AE，且．
（1）求证：直线AE是是的切线；
（2）若，的半径为3，求AD的长．
25．（本小题满分12分）
在学习完《图形的旋转》后，刘老师带领学生开展了一次数学探究活动
【问题情境】
刘老师先引导学生回顾了华东师大版教材七年级下册第121页“探索”部分内容：
如图，将一个三角形纸板绕点A逆时针旋转到达的位置，那么可以得到：
；（ ）
刘老师进一步谈到：图形的旋转蕴含于自然界的运动变化规律中，即“变”中蕴含着“不变”，这是我们解决图形旋转的关键故数学就是一门哲学．
【问题解决】
（1）上述问题情境中“（ ）”处应填理由：____________________；
（2）如图，小王将一个半径为，圆心角为的扇形纸板ABC绕点O逆时针旋转到达扇形纸板的位置．
①请在图中作出点O；
②如果，则在旋转过程中，点B经过的路径长为__________；
【问题拓展】
小李突发奇想，将与（2）中完全相同的两个扇形纸板重叠，一个固定在墙上，使得一边位于水平位置另一个在孤的中点处固定，然后放开纸板，使其摆动到竖直位置时静止此时，两个纸板重叠部分的面积是多少呢？如图所示，请你帮助小李解决这个问题．
26．已知是抛物（b为常数）上的两点，当时，总有
（1）求b的值；
（2）将抛物线平移后得到抛物线．
当0测x2时，探究下列问题：
①若抛物线与抛物线有一个交点，求m的取值范围；
②设抛物线C，与x轴交于A，B两点，与y轴交于点C，抛物线的顶点为点E，外接圆的圆心为点F如果对抛物线上的任意一点P，在抛物线上总存在一点Q，使得点P、Q的纵坐标相等．求EF长的取值范围
参考答案
第I卷（选择题 共30分）
一、选择题：本大题共10小题，每小题3分，共30分．
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | A | C | D | B | C | B | C | A | B | D |
第Ⅱ卷（非选择题 共120分）
二、填空题：本大题共6小题，每小题3分，共18分
11． 12．160 13． 14．16 15． 16．（1） （2）
注：16题第（1）空1分，第（2）空2分．
三、解答题：本大题共10个小题，共102分．解答应写出必要的文字说明，证明过程或演算步骤．
17．解：原式， 6分
=1． 9分
注：第一步含有三个式子的计算，答对一个得2分
18．解：
解法一：①，得② 2分
将②+③，得，解得． 5分
将代入①，得 8分
9分
解法二：由①，得．③ 2分
将③代入②，得，解得． 5分
将代入③，得． 8分
9分
19．证明：， 2分
在和中，
，
． 7分
． 9分
20．（1），
∴四边形ECFD为平行四边形． 2分
又，
∴四边形ECFD为矩形． 4分
（2）过点C作，垂足为H，如图所示
在中，，
． 6分
． 8分
．
∴点C到EF的距离为 10分
21．解：设原计划每天种植梨树x棵 1分
由题可知： 5分
解得： 8分
经检验：是原方程的根，且符合题意． 9分
答：原计划每天种植梨树500棵． 10分
22．解：（1）8 2分
（2）． 5分
（3）列表如下：
| 男1 | 男2 | 女1 | 女2 |
男1 |
| （男1，男2） | （男1，女1） | （男1，女2） |
男2 | （男2，男1） |
| （男2，女1） | （男2，女2） |
女1 | （女1，男1） | （女1，男2） |
| （女1，女2） |
女2 | （女2，男1） |
| （女2，女1） |
|
8分
或树状图：
8分
． 10分
23．解：（1）点在反比例函数的图象上，
． 2分
又点都在一次函数的图象上，
解得 4分
一次函数的解析式为． 5分
（2）对于，当时，．
． 6分
过点A作轴于点H，过点P作轴于点D，如图所示．
，
．
，解得． 8分
点P的纵坐标为2或．
将或代入得或．
∴点或 10分
24．（1）证明：
． 1分
． 2分
． 3分
．
． 4分
，∴AB是的直径
∴AE是是的切线． 5分
（2）作，垂足为E，如图所示． 6分
．
在中，
． 7分
．
在中，． 8分
． 9分
25．解：【问题解决】
（1）旋转前后的图形对应线段相等，对应角相等 2分
（2）①下图中，点O为所求 4分
② 6分
【问题拓展】
解：<方法一>
连结，交AC于M，连结PA，PD，如图所示
．
由旋转得． 7分
在中，
．
在中，
，
，
． 8分
．
．
10分
在和中，
，
又，
．
又，．
<方法二>
连结，交AC于M后，连结，AC交于D，交
点P为的中点，
．
由旋转的性质得：
，
7分
8分
在中，
．
在中，
．
．
在中， 10分
．
．
12分
<方法三>
连结PA，，PD，PC，交AC于M，交于N，如图所示
点P为的中点，
．
由旋转得． 8分
在为中．
．
9分
在中，
10分
． 11分
现证明阴影部分为轴对称图形：连结
点P为的中点，图形的旋转，
．
，
又，
，
在中，．
．
又图形的旋转，∴阴影部分面积被PD等分．
12分
26．解：（1）由题可知： 1分
时，总有，
． 2分
3分
注：如果学生由对称性或者取特殊值直接得出不扣分
（2）①注意到抛物线最大值和开口大小不变，m只影响图象左右平移下面考虑满足题意的两种临界情形：
（i）当抛物线过点时，如图所示，
此时，，解得或（舍）． 4分
（ii）当抛物线过点时，如图所示，
此时，，
解得或（舍） 5分
综上， 6分
②同①考虑满足题意的两种临界情形：
（i）当抛物线过点时，如图所示，
此时，，解得或（舍）． 7分
（ii）当抛物线过点时，如图所示，
此时，，解得或0（舍）． 8分
综上 9分
如图，由圆的性质可知，点E、F在线段AB的垂直平分线上．
令，解得
10分
，
设，
，
，即 11分
．
，即 12分
，
13分
